Concept și calcul infrastructură

Termeni

   Articolul tratează calculul și alcătuirea infrastructurilor pentru modelul structură cu pereți de beton armat. Sistemul de fundare va fi radier general.

   Preluarea și transmiterea încărcărilor ce acționează asupra unei construcții se realizează prin sistemul structural, constituit din trei componente:

• suprastructură (în general, având comportare ductilă);
• infrastructură -substructură și fundații- /sau fundații (comportare în domeniul elastic, cu incursiuni reduse în domeniul plastic);
• terenul de fundare ( comportare în domeniul elastic, cu incursiuni reduse în domeniul plastic).

   Interacțiunea dintre aceste trei componente definește comportarea în totalitate a sistemului la acțiuni. Neglijarea uneia dintre componente prin anumite ipoteze poate duce la rezultate eronate, cum ar fi: nerealizarea mecanismului considerat, amplificare dinamică sau un spor de amortizare datorat terenului, tasarea vecinătăților etc..

Conform  [1], [2] și [3] se definesc:

• substructură: componentă a sistemului structural care prezintă, în raport cu suprastructura, o creștere bruscă, semnificativă de rezistență și rigiditate. Este constituită dintr-un sistem de pereți, dispuși pe înălțimea subsolului (sau subsolurilor), care conlucrează cu planșeele care îi mărginesc sau pe care le străbat. În anumite situații substructura include și primul sau primele niveluri peste cota zero.
• fundație: parte inferioară a unei construcții care are rol de a transmite încărcările la teren și de a participa, alături de celelalte elemente structurale la asigurarea rezistenței, stabilității, exploatării și durabilității construcției. În cazurile în care există o substructură, aceasta conlucrează cu fundațiile, prin intermediul cărora reazămă pe teren, formând o unică componentă.  În cazul în care suprastructura reazămă direct pe teren, prin intermediul fundațiilor (grinzi de fundare - tălpi continue, fundații izolate etc., construcții fără subsol) se va face referire numai la termenul de fundație.
• infrastructură: ansamblul format dintre substructură și fundație. Situată de regulă sub cota zero a construcției.
• fundație de suprafață directă: fundația la care încărcările transmise de structură sunt preluate exclusiv prin contactul dintre baza fundației și teren.
• fundație de suprafață semi-încastrată: fundația la care încărcările transmise de structură sunt preluate atât prin contactul dintre baza fundației și teren cât și prin suprafața laterală în contact cu terenul.
• teren (de fundare): pământ, rocă sau material de umplutură care există pe amplasament înainte de execuția lucrărilor de construcție. Terenul de fundare se consideră pe întreaga zonă de influență a bulbului de presiune.

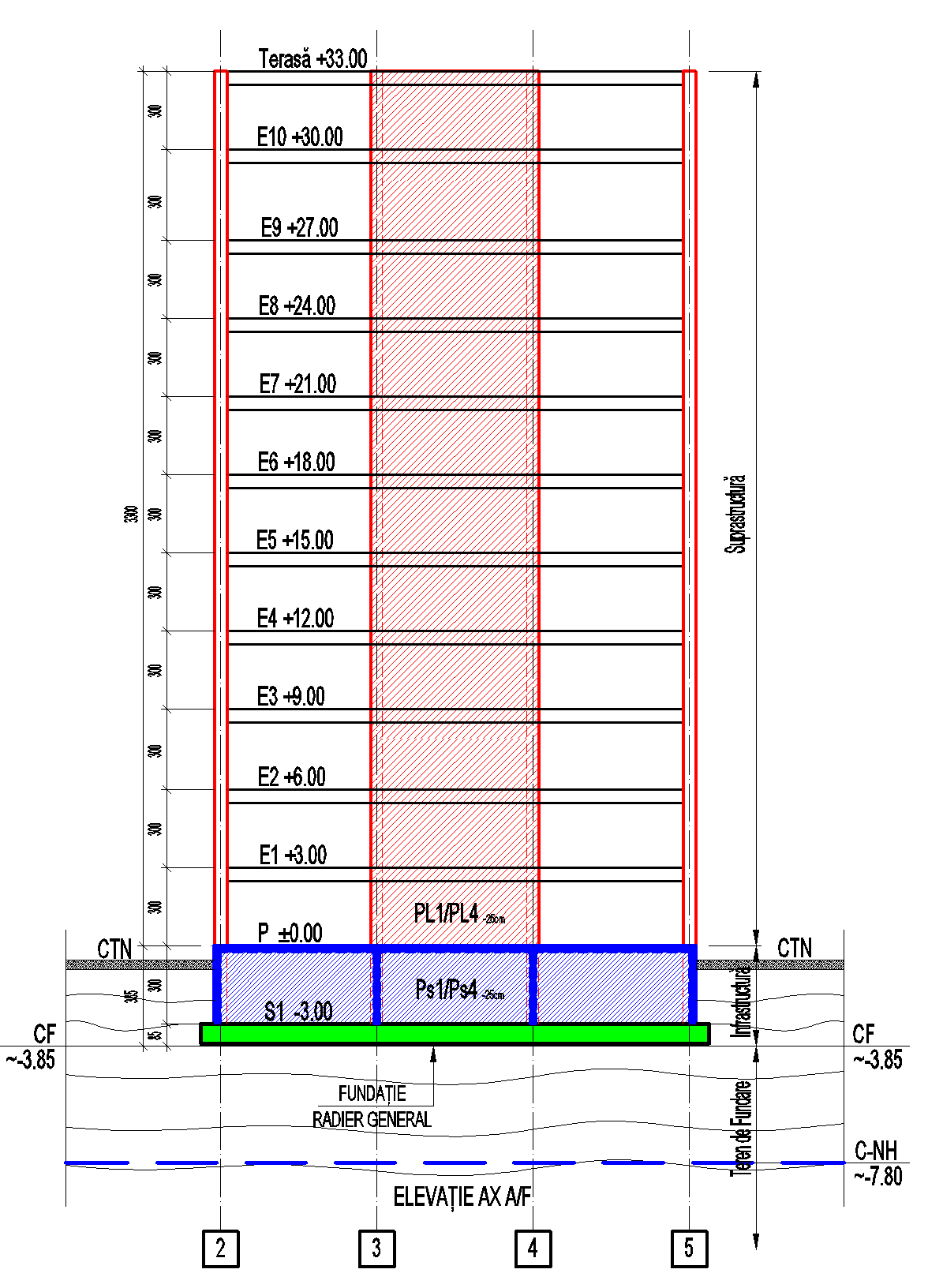
Alcătuire și concept

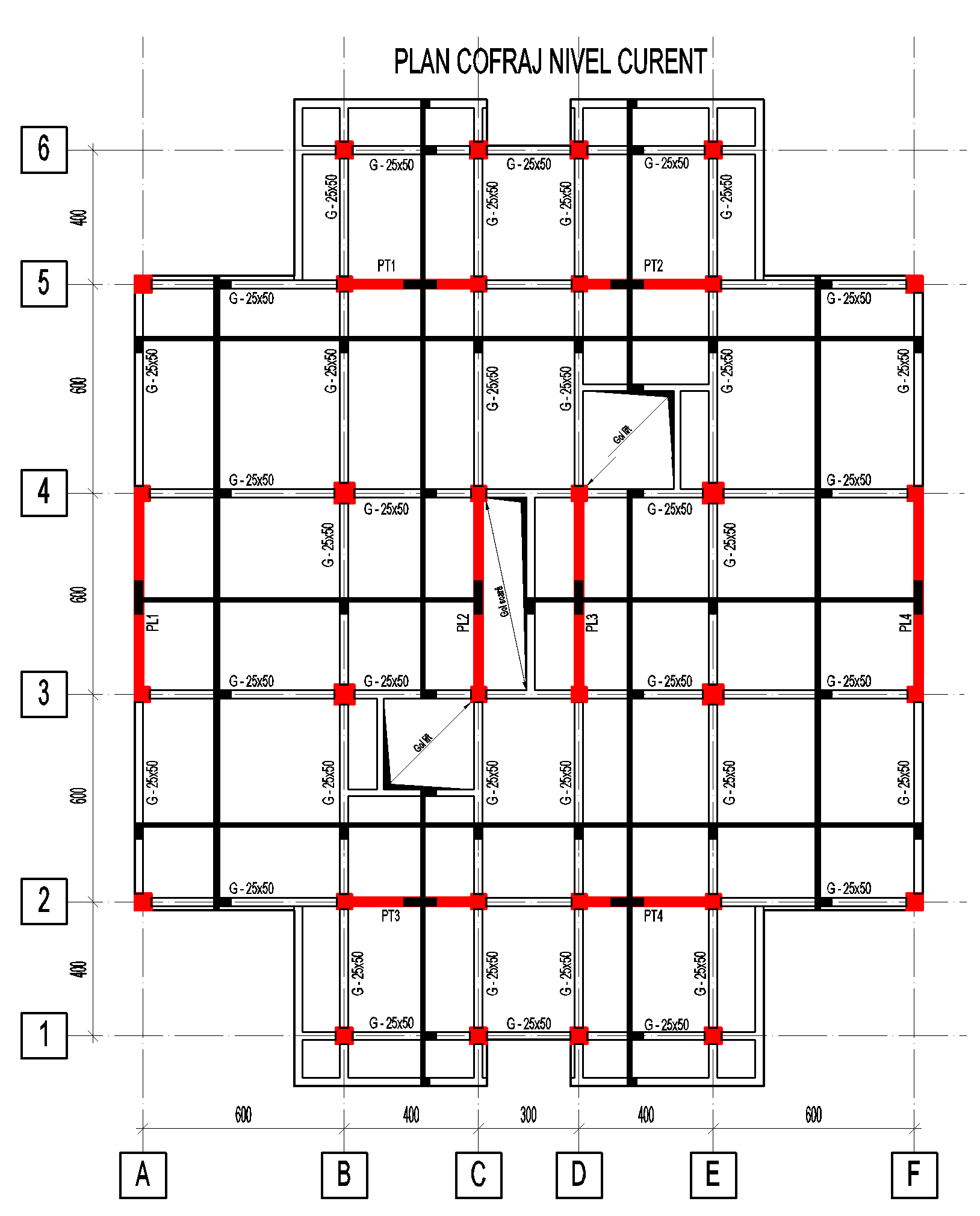
   Zona de infrastructură se dimensionează să aibe un răspuns cvasielastic, astfel fiecare element al infrastructurii trebuie să fie capabil să preia solicitările generate de suprarezistența suprastructurii. Alcătuirea infrastructurilor va urmări elementele din suprastructură astfel încât traiectoria încărcărilor să fie liniară. Pereții perimetrali vor asigura o suprafață plană în vederea realizării hidroizolației și continuității acesteia. Se vor evita, pe cât posibil, elememte ce ies în afara planului determinat de pereții perimetrali, acestea ducând la apariția de colțuri și implicit o execuție mai dificilă la realizarea hidroizolațiilor.  

   Dispunerea de pereți intermediari se va face de câte ori arhitectura o permite, aceștia vor "lega"  pereții suprastructurii pe zona de infrastructură, asigurând o rigiditate suficientă și o suprarezistență a infrastructurii. Prin dispunerea acestor pereți se poate asigura o distribuție uniformă a presiunilor, prin efecte de suspendare. Se recomandă ca cel puțin pereții ce au solicitări puternice în suprastructură să fie "legați" în infrastructură. Printr-un număr suficient de pereți se poate reduce dimensiunea radierului și a plăcii de la cota de "încastrare" a suprastructurii (±0.00). 

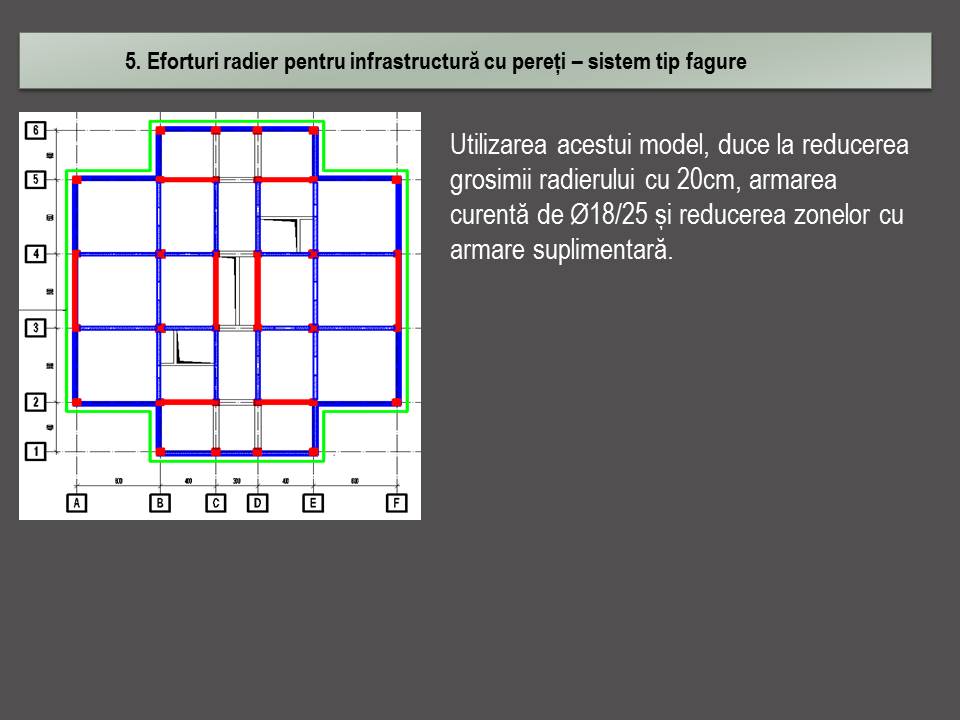
   Se vor expune două soluții, una la care infrastructura nu are pereți interiori suplimentari față de suprastructură și o soluție la care s-au introdus pereți suplimentari. Tipul 1 de infrastructură urmărește planul de cofraj curent și având pereți de contur. Cu verde este reprezentat conturul radierului.

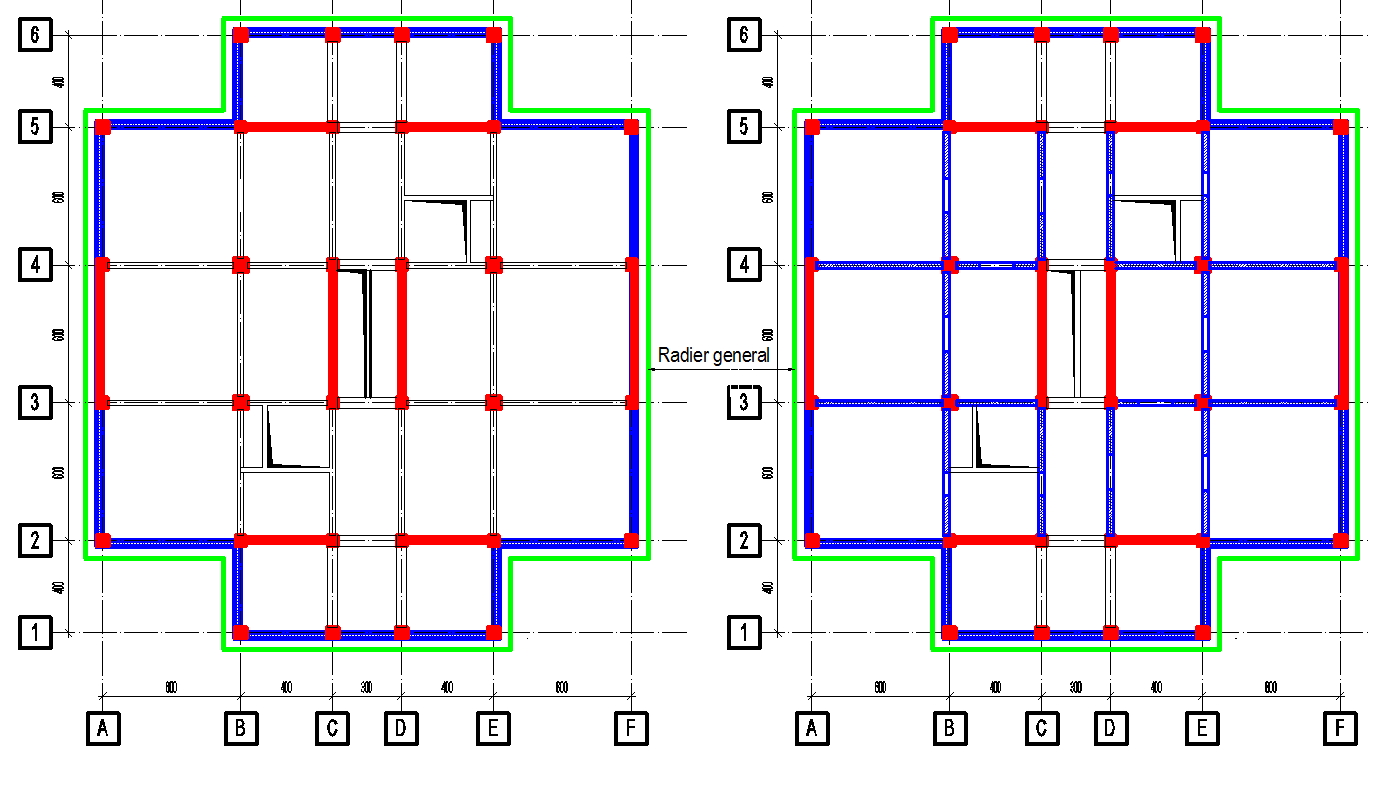
   Calculul elementelor infrastructurii se va face cu valorile de calcul a rezistențelor materialelor. Infrastructura se va calcula la starea de mobilizare a mecanismului din suprastructură, pentru solicitarea seismică. Starea de eforturi la nivelul infrastructurii, în cazul solicitărilor seismice, se poate obține într-un mod simplificat prin amplificarea forțelor seismice de proiectare cu un factor de suprarezistență.

F_h=γ_RdΩ_medF_b , dar γ_RdΩ_med≤1.50

Se pot întâlni situații în care γ_RdΩ_med poate avea valoare mai mare de 1.50. Este recomandat să se facă o evaluare succintă a coeficientului γ_RdΩ_med.

γ_Rd=1/1.10, pentru structuri încadrate în clasa M de ductilitate și la care factorul de comportare q≤3;

γ_Rd=1.20/1.30, pentru structuri încadrate în clasa H de ductilitate și la care factorul de comportare q>3;

γ_Rd - factor ce ține seama de diferitele surse de suprarezistență (oțel, beton utilizat etc.).

Ω_med - un parametru global ce ține seama de eforturile capabile ale elementelor și eforturile secționale ale acestor în situația de proiectare seismică, unde Ω_i≤q.

Această aproximare nu ține seama de redundanța sistemului, de distribuția și modul de plastificare a elementelor verticale, calculul realizându-se pe modele elastice. O abordare mai apropiată presupune realizarea unei analize neliniare, astfel se pot determina și eventualele suprasolicitări ale pereților și planșeelor infrastructurii.

Calculul va ține seama de  interacțiunea teren-structură, proprietățile terenului se vor exprima prin legi de deformare elastică sau prin legi constitutive mai riguroase, astfel încât resorturile care modelează terenul să poată fi definite prin legi liniare sau neliniare. În cazul structurilor cu un număr mai mare de 2 subsoluri, regim de înălțime mai mare de 6m se va ține seama de presiunile active și pasive ale terenului.

Conform [2], se recomandă ca la proiectare să se prevadă măsuri pentru a asigura elementelor infrastructurii o capacitate minimă de deformare în domeniul plastic, astfel adoptarea unor reguli constructive confrom P100-1 similare structurilor cu ductilitate medie - DCM- fiind una din soluții.

Calcul substructură - placă și pereți

Condiții constructive și calcul planșeu

Planșeul peste subsol, spre deosebire de planșeele nivelurilor curente, reprezintă o componentă importantă, mai ales în realizarea noțiunii de "cutie rigidă". Acesta participă la realizarea efectului de "menghină", asigură redistribuția forțelor orizontale între pereții din suprastructură și infrastructură și preia încărcările perpendiculare pe planul său.

Conform normelor de proiectare sunt recomandate următoarele:

 În prima etapă se va determina armarea plăcii la solicitări perpendiculare pe planul acesteia (la acțiuni permanente și variabile de la nivelul planșeului). Armarea centurilor va rezulta din efectul de grindă perete a planșeului la solicitări în planul său și/sau din eforturile de suspendare generate de elementele din suprastructură. În plus, armarea centurii poate fi dimensionată și din efectul de grindă perete generat de solicitările în planul peretelui din gruparea fundamentală sau cea seismică.

Condiții constructive centură

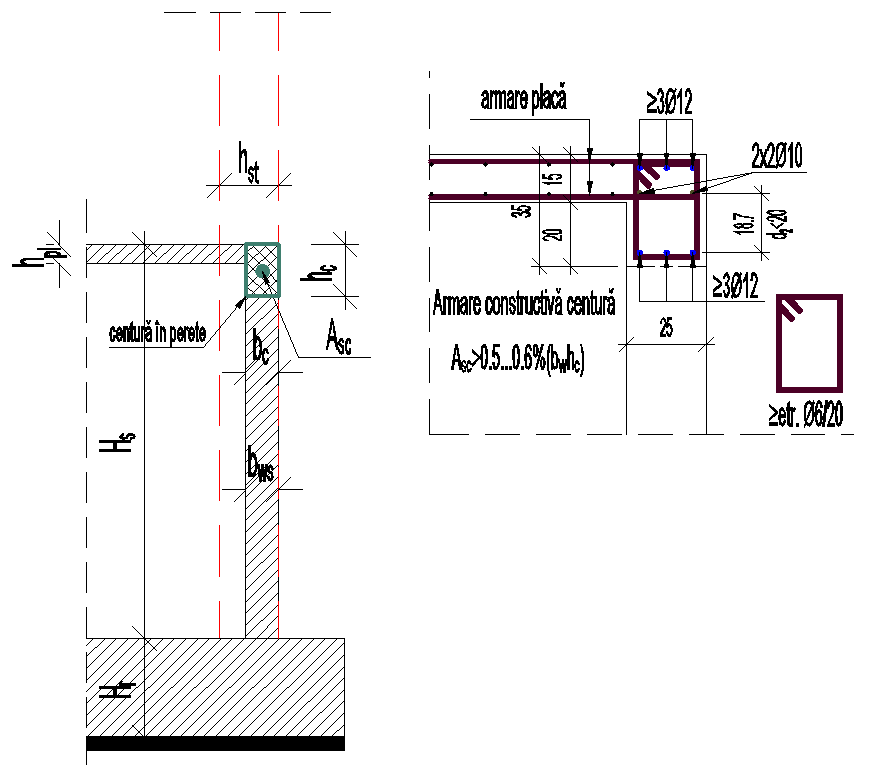
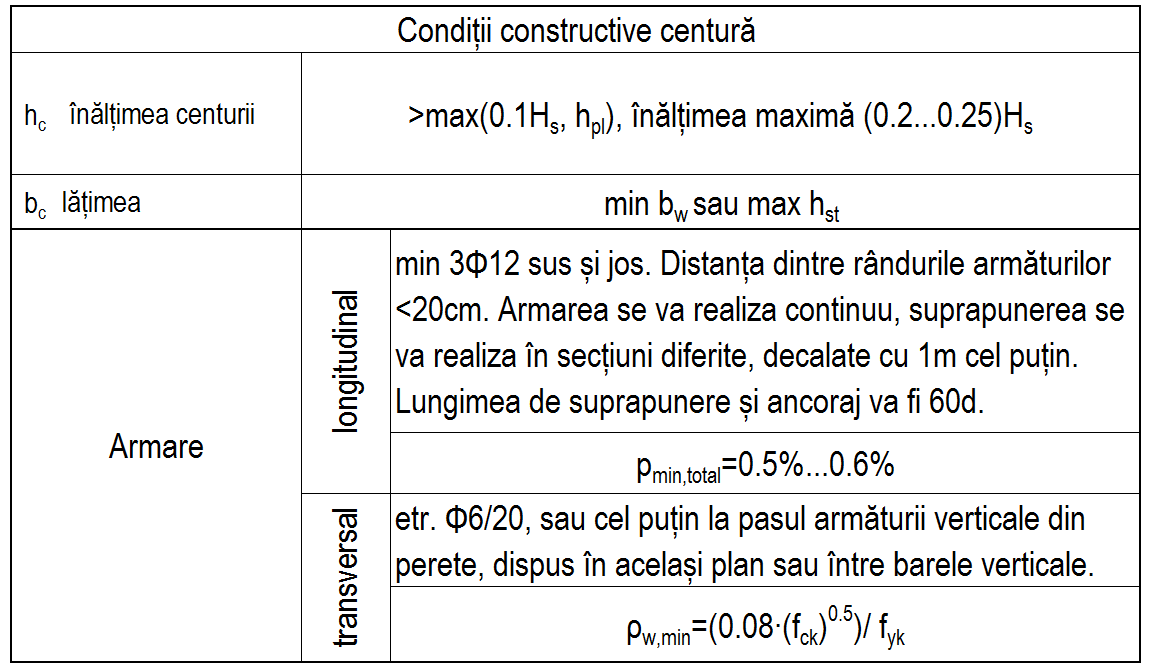
Condițiile constructive sunt valabile doar pentru centura peste subsol. Pentru restul centurilor se vor avea în vedere condițiile de la 8.5.5 [1].

Pentru calcul se va folosi oțel Bst 500 și beton C25/30. Astfel pentru armarea minimă propusă 6Φ12+2Φ10=835mm² rezultă o capacitate la întindere de 363kN (36,3to). Pentru condițiile considerate armarea minimă transversală asigură un procent minim de armare de 0.11%>0.08%. Barele Ø10 se pot dispune la intradosul armăturii inferioare din placa , având dublu rol (constructiv și de rezistență).

Verificarea condiției de rigiditate a planșeului

Ținând seama că deplasările la bază sunt reduse, acestea se pot considera nule, astfel deplasările efective de la nivelul planșeului peste subsol vor fi și cele efective.

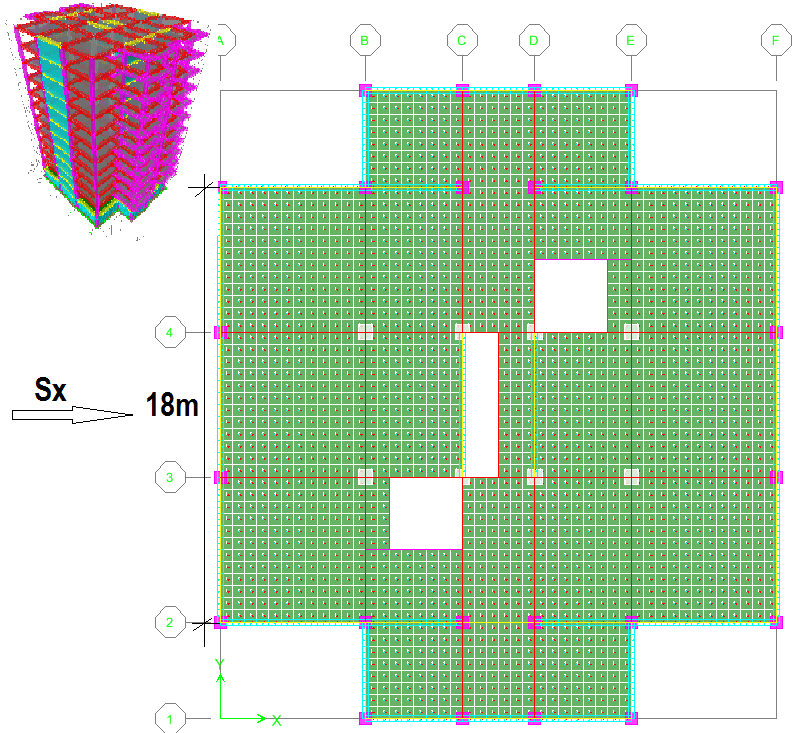
 Forțele de inerție generate la nivelul suprastructurii pentru acțiuni considerate pe direcția principală X-X vor fi în proporție de peste 70% "concentrate"  în pereții cuplați. Conform configurației infrastructurii, acești pereții "beneficiază" de elemente de continuitate în subsol, astfel transferul forțelor de inerție se face relativ direct, nu prin intermediul planșeului, considerarea unui model cu forțe distribuite pe una din laturi va fi destul de acoperitoare în dimensionarea planșeului.

Verificare rigiditate planșeu:   

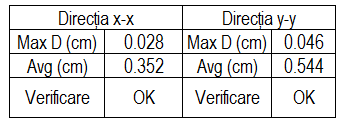
În general această condiție, de deplasare maximă, este îndeplinită pentru planșeul peste subsol la structurile curente, cu deschideri de 6m, fără goluri mari în planșeu. Grosimea planșeului putând fi dictată din alte considerente, de rezistență, vibrații etc.. Grosimea plăcii de la cota ±0.00(zona de încastrare) poate influența efectul de cutie rigidă, comportarea de menghină și de încastrare a suprastructurii în cazul construcțiilor cu mai multe subsoluri. Un caz particular îl constituie planșeul ultimului nivel sau cel al structurilor parter cu deschideri mai mari de 6x6m, unde se recomandă această verificare.  

Calculul și verificarea condițiilor de rezistență a planșeului

a. Model de grindă perete

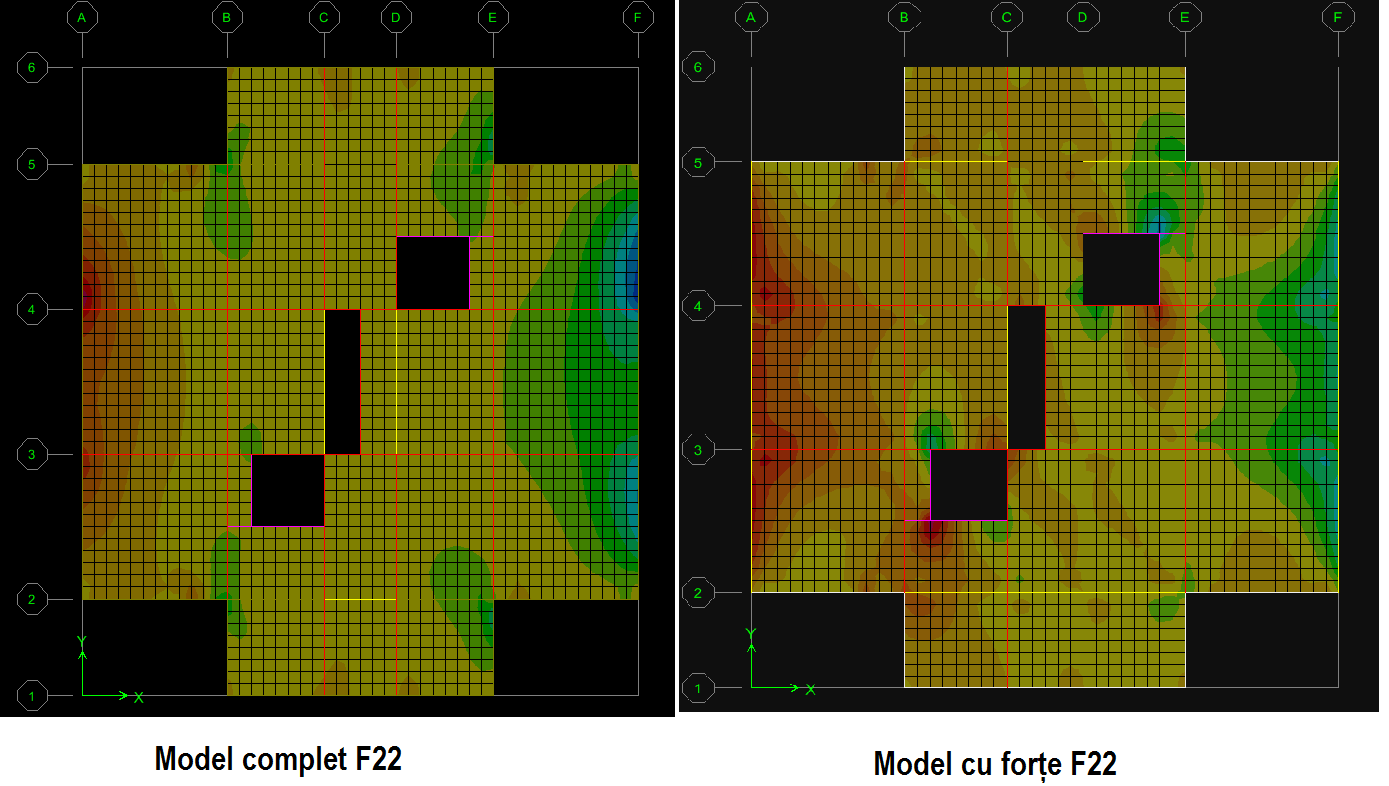
Armarea din încovoierea de ansamblu a planșeului va fi :

ax A/F (SX): A_s=F₂₂/f_yd=470/425=1080mm^₂⇒6Φ14+2Φ12=1150mm².

ax 2/3 (SY): A_s=F₁₁/f_yd=510/425=1170mm2⇒6Φ14+2Φ14=1232mm².

F₂₂, F₁₁ se determină printr-o mediere la fața peretelui de la subsol (albastru reprezintă zona întinsă).  

Modelul cu forțe a presupus distribuirea forțelor pe cele două laturi. Elementele intermediare, stâlpi și grinzi, ce realizează cadre pe direcția axelor asigură și rigiditatea planșeului la voalare, modelul se poate asocia și cu cel al inimii grinzilor metalice înalte.

Model de calcul planșeu direcția x-x (rotit):

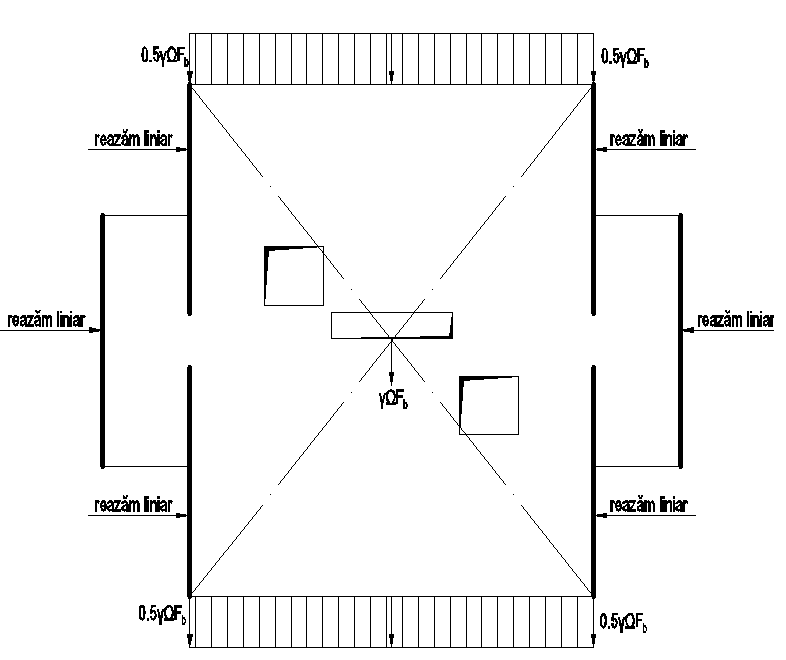
 Dacă modelul nu prezintă diferențe pentru eforturile σ_z-z, pentru σ_y-y sunt total diferite datorită schemei de calcul pentru încărcare. Ceea ce nu este real, ținând seama de poziționarea pereților care aduc aceste încărcări.

b. Model strut and tie

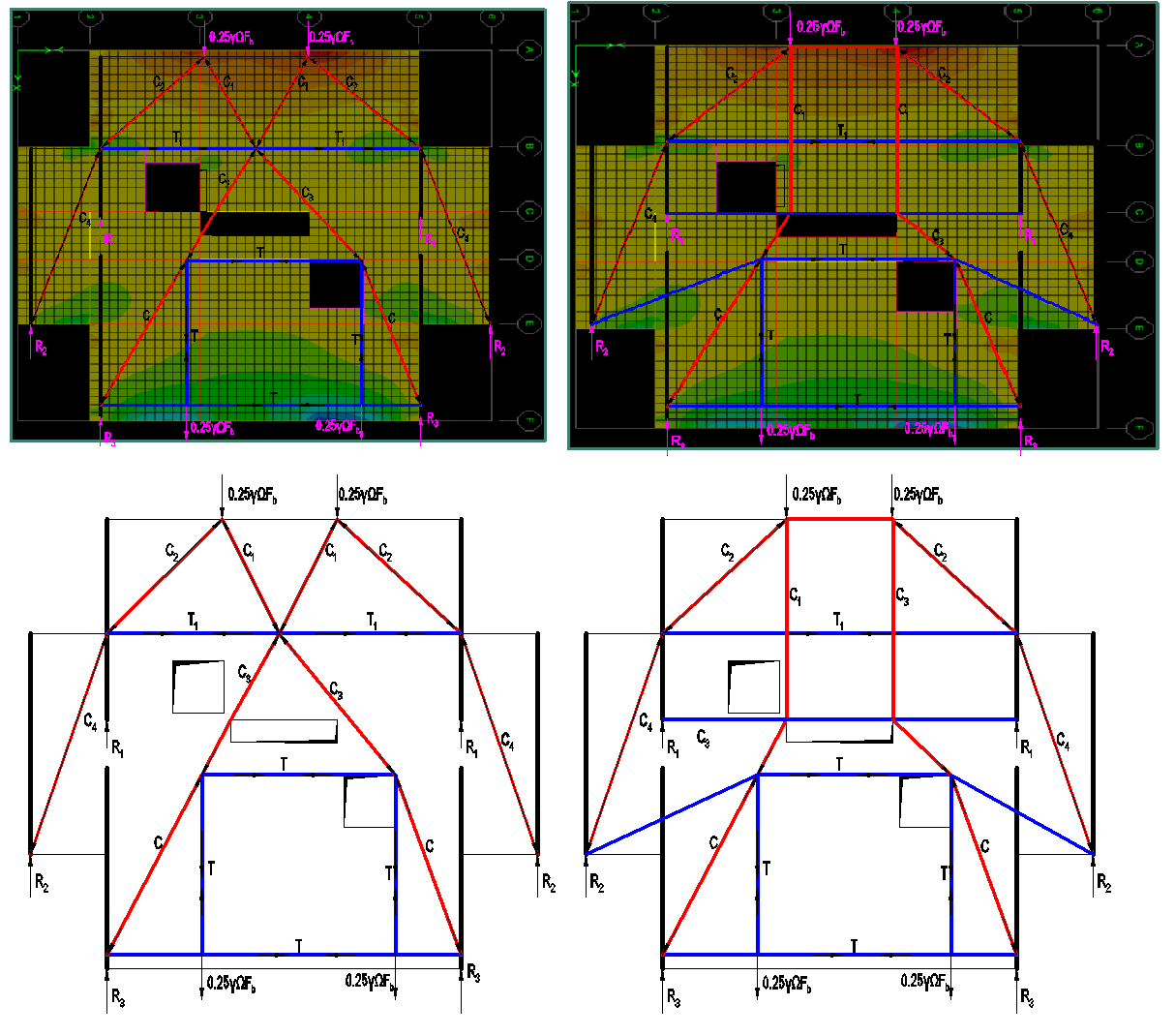
 Utilizarea acestui model pentru calculul planșeelor nu este atât de folosit la proiectarea curentă a acestora, datorită complexității și volumului mare de calcul. În general ele oferă informații despre poziția și distribuția armăturilor principale, vizualizarea distribuției de forțe. Modelele prezentate nu sunt unice, se recomandă ca modelul să urmeze îndeaproape distribuția eforturilor indicată de un model elastic. Dacă se utilizează un unic model și armarea se realizează după acesta se poate ajunge la redistribuții importante de eforturi și la deschiderea excesivă a fisurilor.

O contribuție importantă o au grinzile de cadru care îndeplinesc rol atât de tiranți cât și de biele, ceea ce asigură o distribuție uniformă de eforturi, evitându-se concentrarea de eforturi în placă. 

La calculul planșeului metoda elementului finit (elemente de suprafață, shell-uri) oferă rezultate satisfăcătoare pentru dimensionare și verificare.

c)  Calculul planșeului la forțe aplicate local în planul său

Conform [1], transmiterea forțelor orizontale din planul planșeului la pereți se poate face prin:

- compresiune directă pe capul peretelui (mecanismul 1, F1);

- armături întinse care "colectează" forțele distribuite pe inima grinzilor pereți a planșeului, aferente peretelui (mecanismul 2, F2);

- lunecări între inima peretelui și planșeu (mecanismul 3, F3);

Astfel forța tăietoare din pereți provenită de la planșeu prin cele trei mecanisme, F_pl=F₁+F₂+2F₃

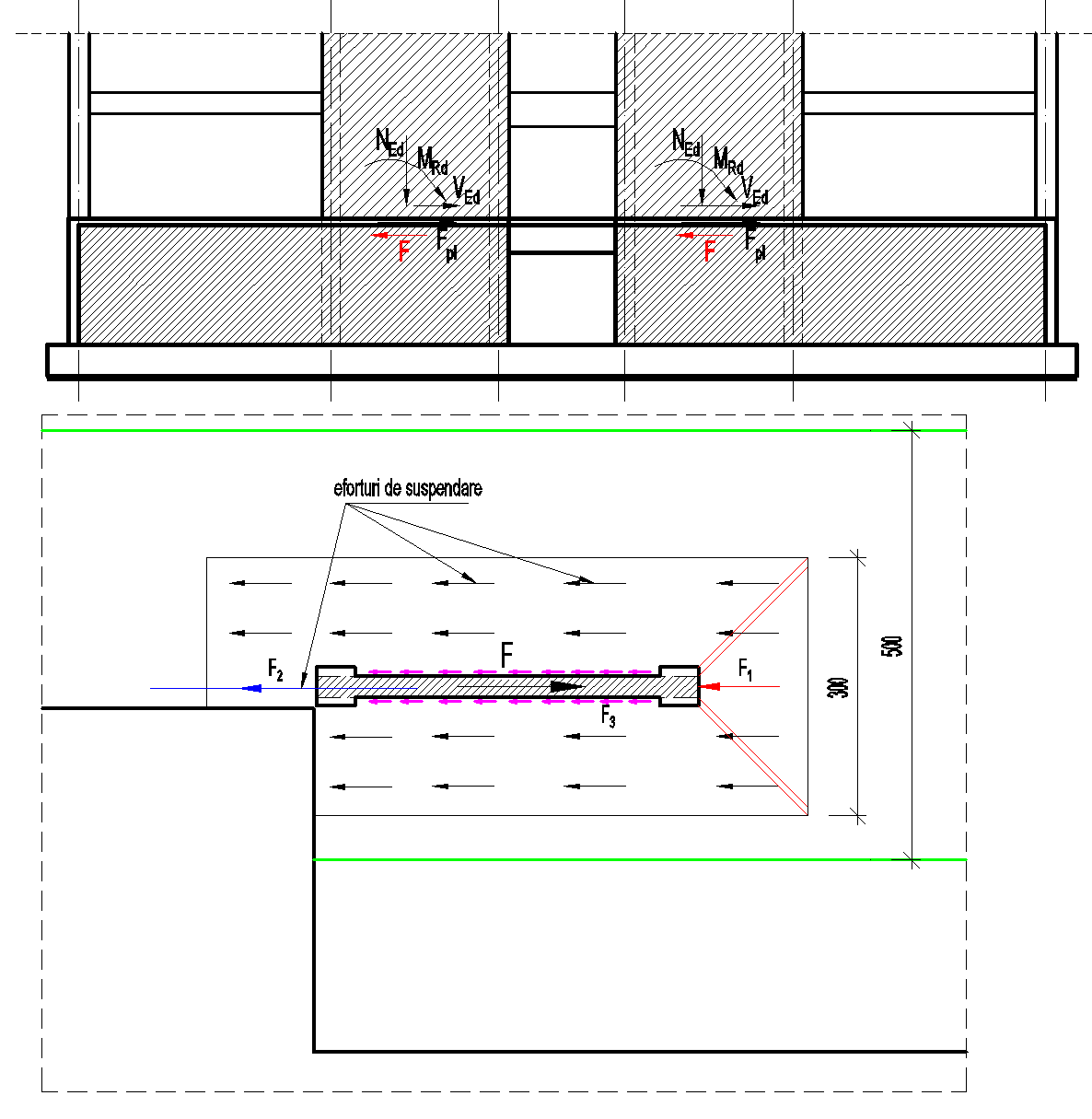
 Transmiterea eforturilor pereților din suprastructură la cei din infrastructură este ceva mai complexă, aceasta se realizează prin eforturi de întindere în armătură, eforturi de compresiune, eforturi de lunecare și eforturi de suspendare. Eforturile de suspendare de la nivelul planșeului se pot determina din eforturile date de shell-uri pe direcția de solicitare (F₁₁ x-x, F₂₂ y-y).

Pentru pereții transversali: efortul de suspendare este de 605kN, astfel armarea centurii din axele 2 și 5 va fi de 6∅16+2∅12→622kN

Pentru pereții longitudinali: efortul de suspendare este de 750kN, astfel armarea centurii din axele A și F va fi de 6∅20+2∅12→868kN

Armarea centurilor va fi dimensionată o dată pentru încovoierea planșeului și apoi pentru eforturi de suspendare, acestea nu se suprapun, solicitările fiind diferite pentru aceeași centură. Dimensionarea centurilor din efectul de grindă perete a pereților de subsol la încărcări aplicate în planul lor se va face conform schemei de mai jos.

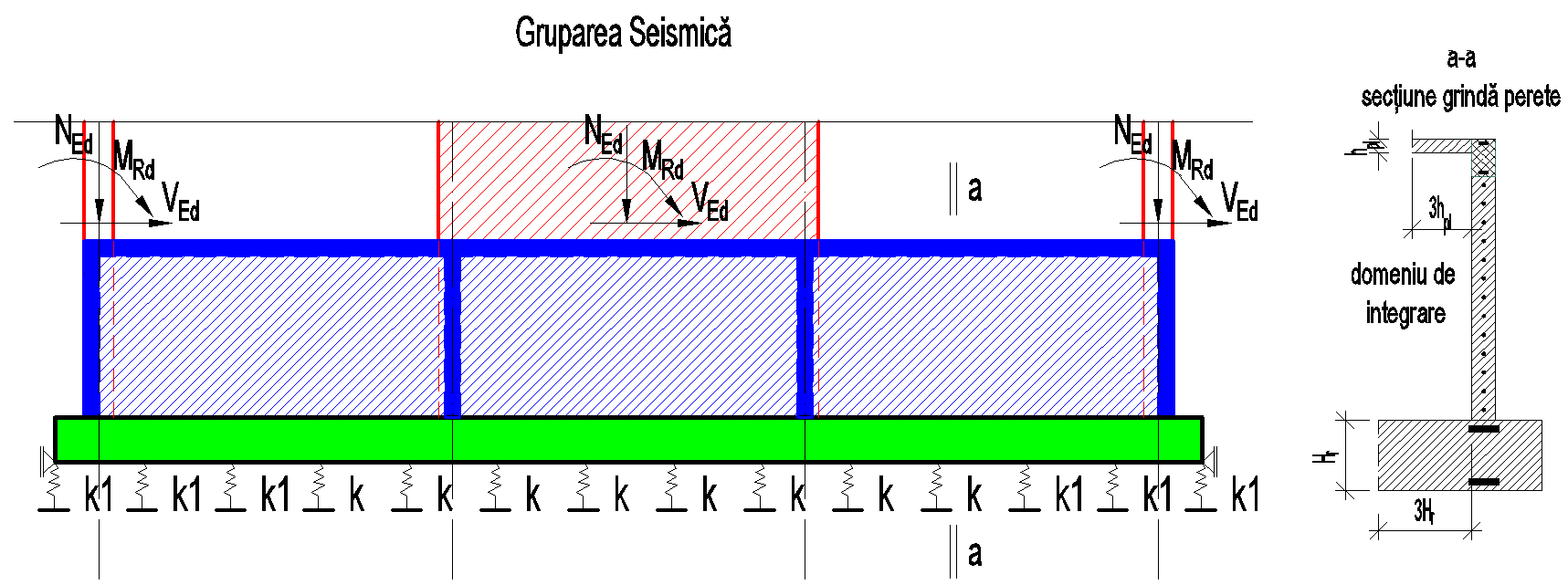Pentru domeniul de integrare, când se utilizează elemente shell, se poate accepta doar inima peretelui.

Condiții constructive și calcul pereți

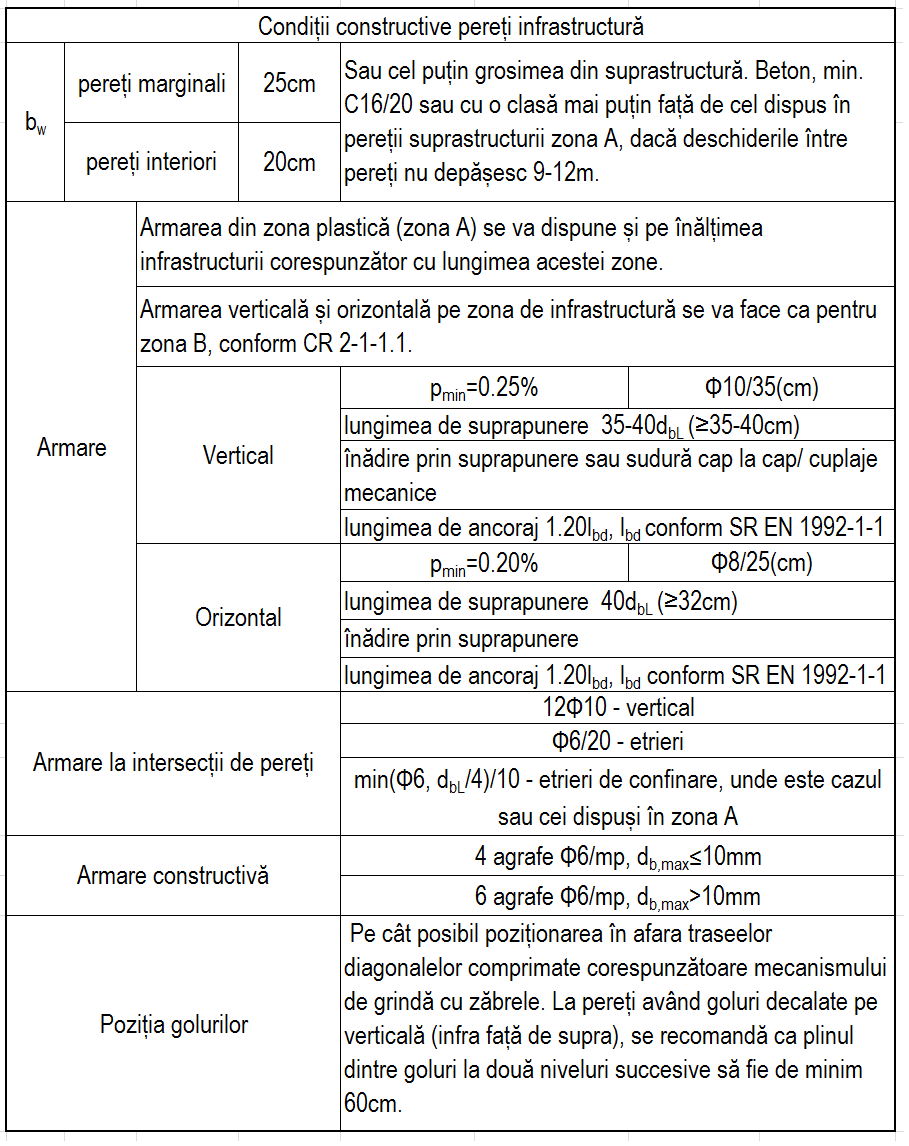
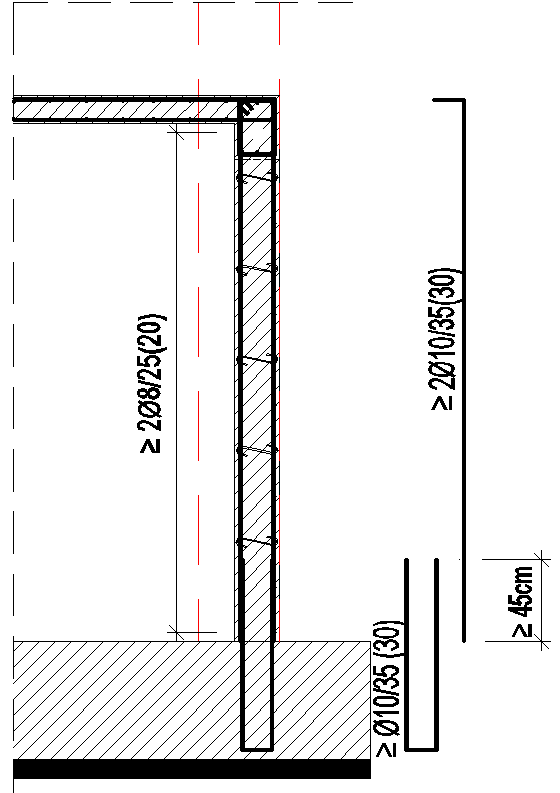
 Capacitatea pereților de la nivelul infrastructurii se va determina ținându-se seama că aceștia sunt pereți scurți, în calculul de rezistență se va ține seama și de contribuția armăturii verticale. Forțele de suspendare (tăietoare și lunecare) vor fi preluate de planșeu, astfel pe lângă armătura din centură va intra în lucru și o parte din armătura planșeului dispusă în lungul peretelui. 

Calcul perete de subsol ax 2 și 5:

Forța de proiectare pentru PT1 - V_Ed=1522kN și PT2 - V_Ed=2738kN, acestea vor fi transmise la nivelul pereților infrastructurii prin intermediul armăturii de colectare. Aceste forțe sunt cele asociate mecanismului de plastificare propus.

Model strut and tie

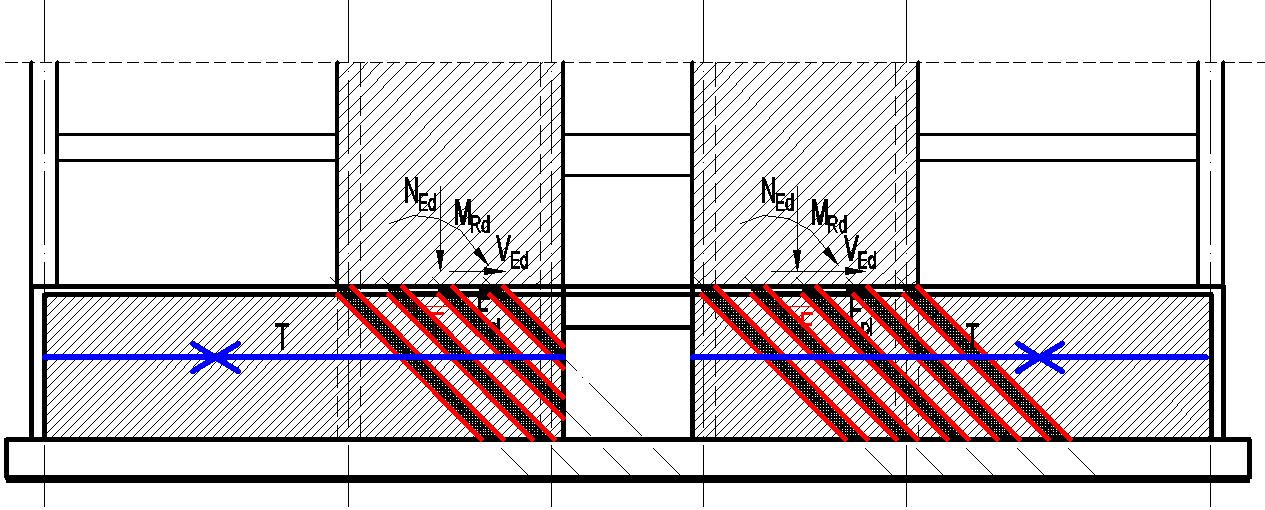
 Armarea transversală propusă pe zona plastică fiind 2∅12/15. Pe zona de infrastuctură, pentru axele 2 și 5,  se va propune o armare de 2∅10/15 orizontal și vertical 2∅10/20.

Forța tăietoare capabilă:

    

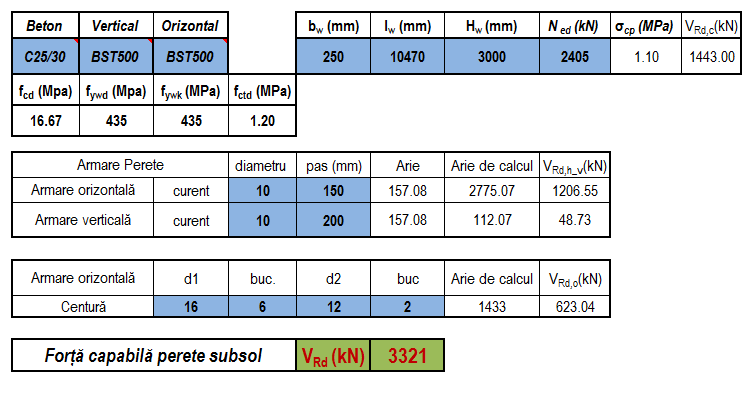
 În mod similar se face calculul și pentru peretele din axul A și F. În mod curent, ca armare orizontală se va utiliza armarea din zona plastică. Sunt situații unde aceasta se poate reduce datorită dezvoltării pereților pe zona infrastructurii. 

Condițiile minime impuse prin conformare asigură rezistența necesară pereților de subsol pentru multe tipuri de structuri.

Calcul și alcătuire fundație - radier general

Condiții constructive radier

 

 

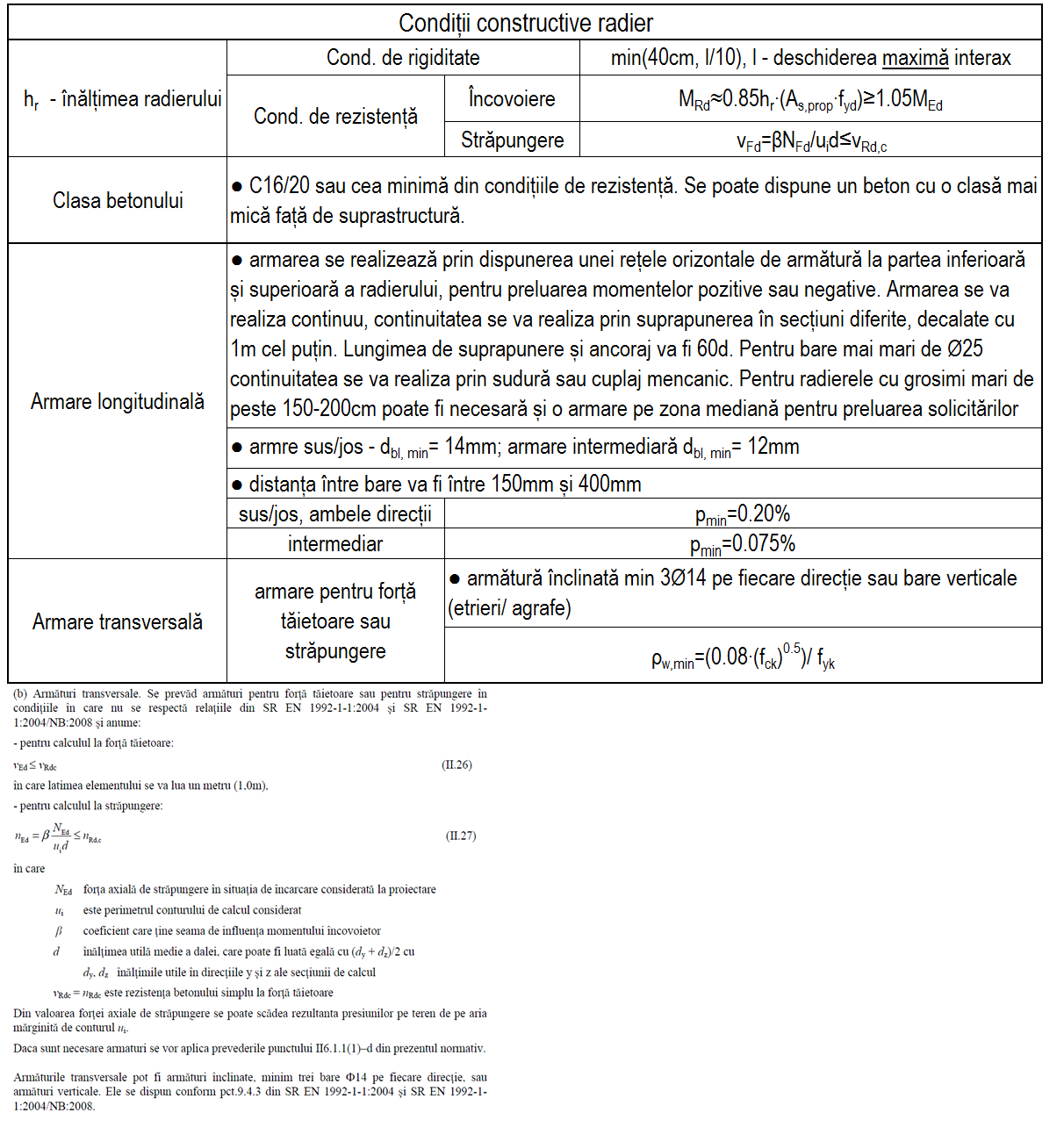
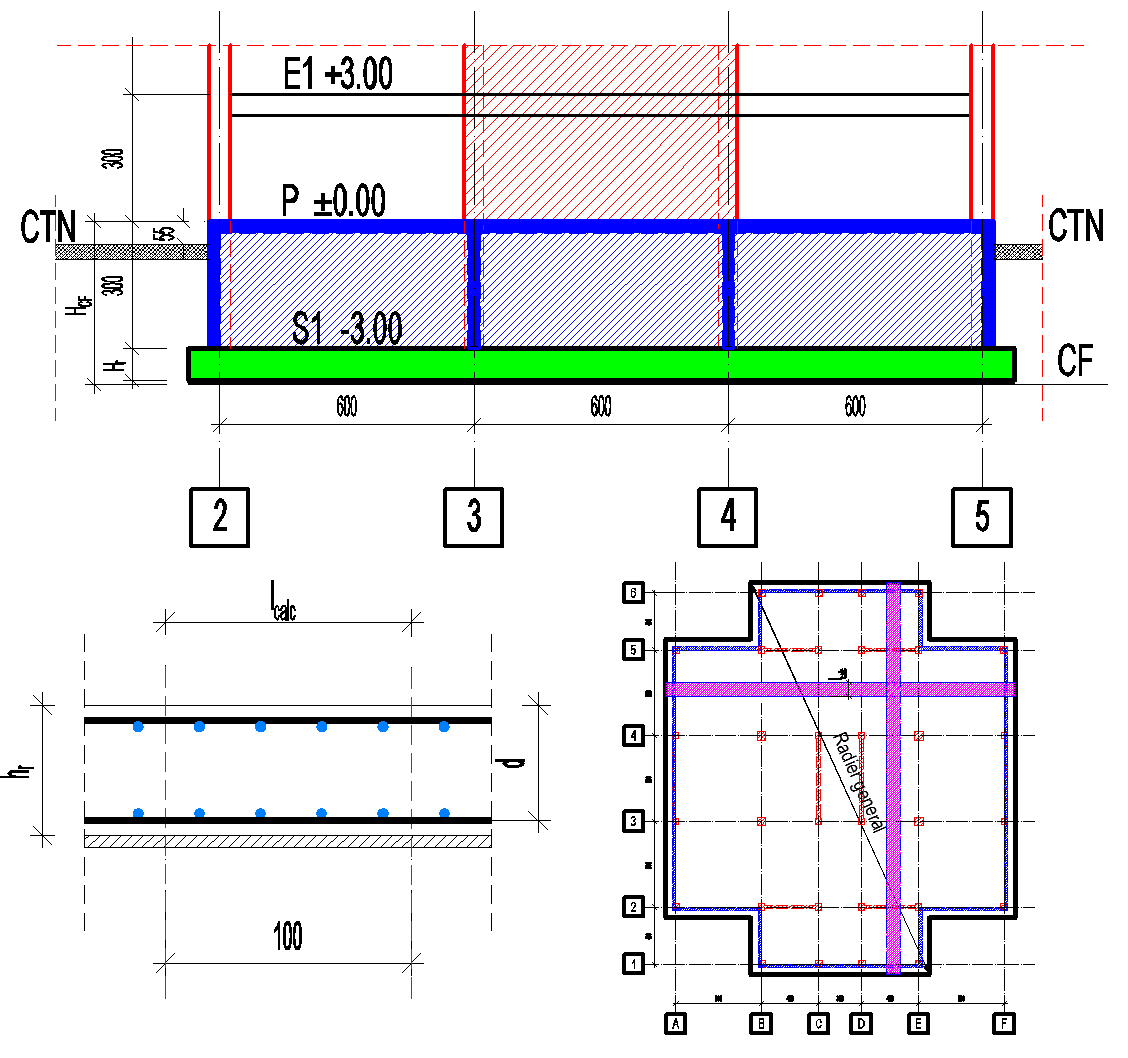
 Calculul radierului ca fundație directă urmează procedura din NP 112, "Normativ privind proiectarea fundațiilor de suprafață", dar și procedurile legate de plăci groase amplasate pe teren. Calculul pentru determinarea stării de eforturi și calculul de rezistență se va face ținându-se seama de caracteristicile terenului de fundare și a modului de comportare a acestuia în prezența acțiunilor aduse de structură. Calculul se va desfășura pe metru liniar de radier, similar plăcilor.

Fundațiile au o cerință mare de rigiditate și rezistență astfel, o abordare pentru predimensionarea și calculul radierulului presupune dimensionarea armăturii din condiții constructive (la procent) pe cât posibil. În ceea ce privește armarea, se recomandă utilizarea unor diametre mai mari la pas mai rar, de exemplu: pentru Ø16/10 se poate folosi Ø25/25 sau Ø20/15. A se evita pe cât posibil distanțe de sub 150mm între bare pe întreaga suprafață a radierului. Aspectul tehnologic, în ceea ce privește utilizarea armării cu bare ce realizează plase cu ochiuri mari (250...400mm), duce la realizarea unor platforme de lucru.

Pentru un radier cu grosimea de 40cm, armarea din procent minim 0,20% pe ambele fețe și direcții, duce la un procent total de 0.80%, pentru 1mc fiind un consum de 80-85kg/mc (Ø16/15- pe toate direcțiile). 

Condiția de rigiditate

Condiția de rigiditate are în vedere două aspecte importante: i) distribuția uniformă a presiunilor la nivelul terenului (în gruparea fundamentală p_med≤1.20·p_conv, p_max<p_pl); ii) limitarea tasărilor diferențiate între zonele de aplicare a încărcărilor (tasarea relativă între două puncte Δ_s≤ 6...2/1000)

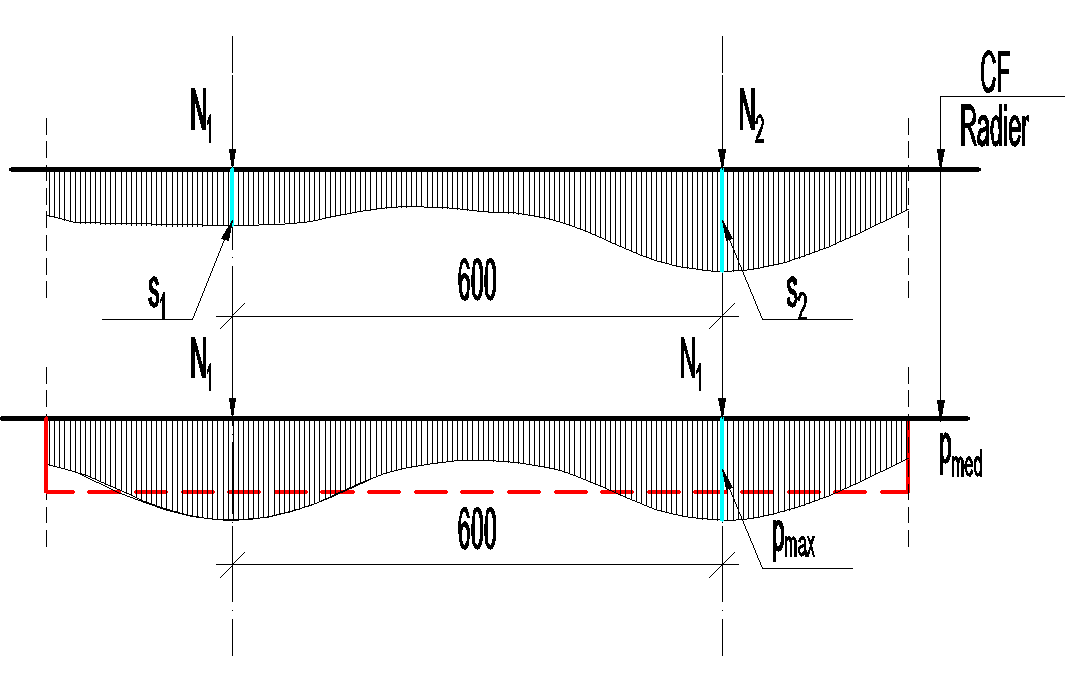
Δ_s=(s₂-s₁)/l, în cazul de față l=600cm. În mod curent condiția l/10, pentru terenuri uzuale, asigură o predimensionare suficientă pentru calculul inițial. Pentru modelul considerat se poate pleca de la o dimensiune de 60cm pentru grosimea radierului.

Condiția de rezistență

Încovoiere: p_min=0.20%⇒Ø16/15⇒M_Rd≅0.85·600·201·435·10^₃⁄150= 297 kNm/m (consum de armătură 83...85kg/mc). Momentul capabil din condiția de rezistență, pentru situația de predimensionare, ținând seama de condițiile minime constructive: diametru armătură Ø16>Ø14; distanța între bare (pas armătură) 150mm=150mm<400mm.

Ținând seama de condițiile de încărcare, pe anumite zone radierul se poate îngroșa pentru a răspunde cerințelor de rigiditate și rezistență, acolo unde nu se impune o grosime unitară.

Străpungere: Calculul la străpungere este similar cu cel pentru planșeu dală fără vută (dacă radierul nu este vutat), în același timp se va ține seama de reacțiunea terenului (presiunea medie din perimetrul de calcul).

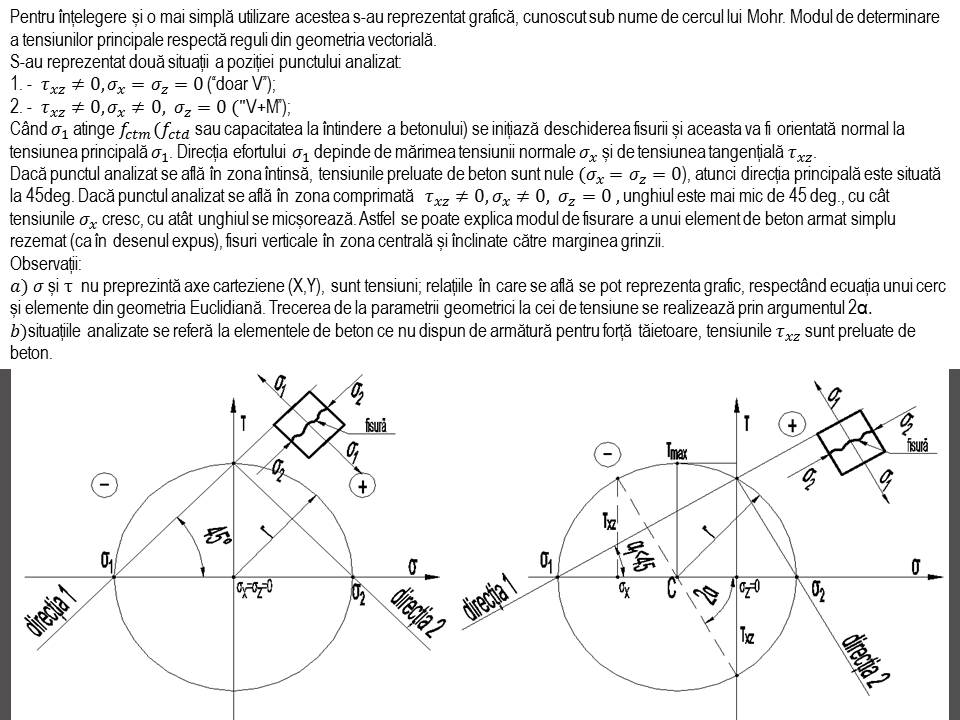
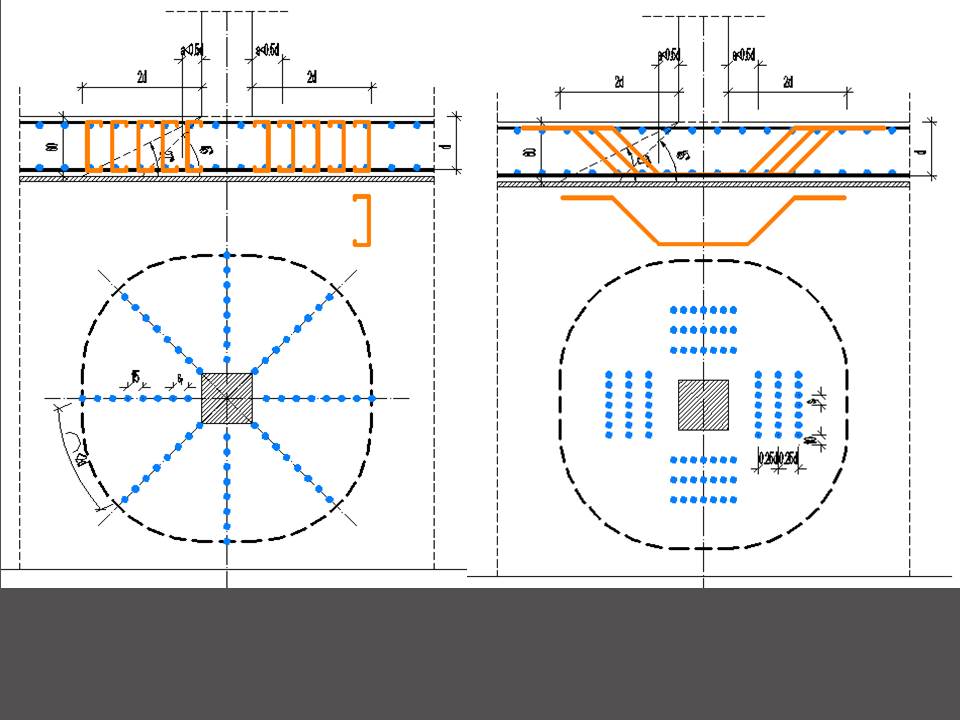
Prezentare calcul la străpungere radier și fișier calcul numeric. 

Date teren de fundare

La nivelul cotei de fundare s-au considerat:

 

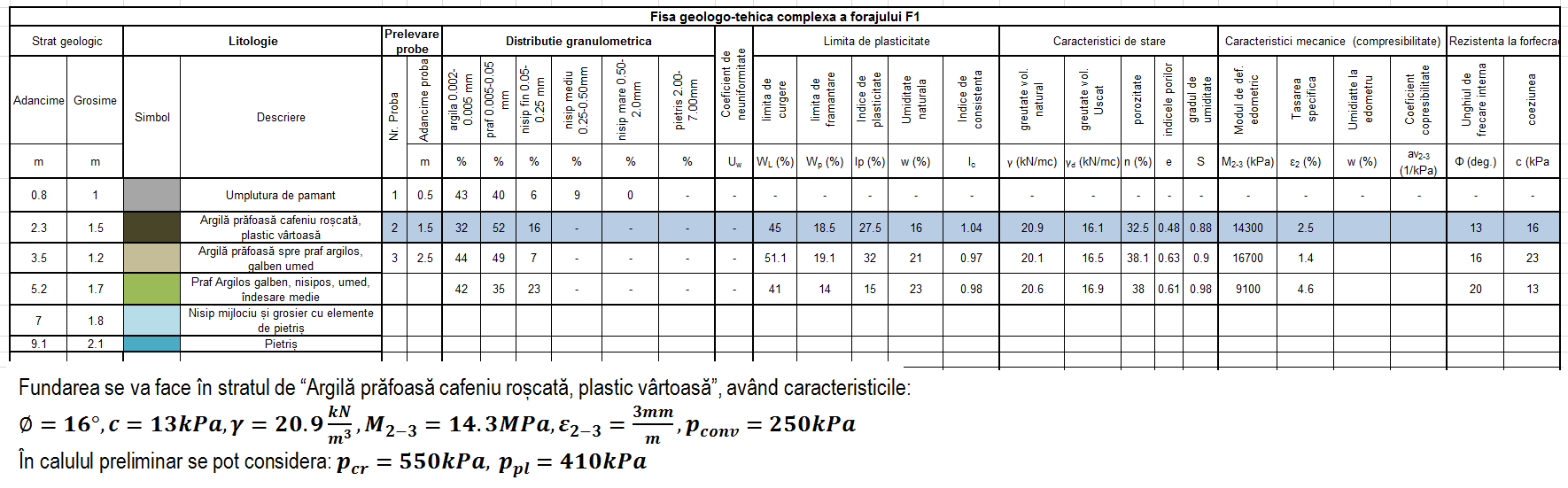
Calcul și verificare radier

Starea de eforturi în radier (M+V) se stabilește printr-un calcul liniar de placă (radier) pe mediu elastic (Winkler). Parametrul esențial pentru calculul eforturilor este dat de coeficientul de pat (rigiditatea terenului) ks. Acesta se stabilește pentru cele două grupări (GF și GS), având valori diferite. Datorită incertitudinilor mari în stabilirea coeficientul de pat  pentru gruparea specială, se vor determina eforturile pentru 3 situații (min, med, max) ale parametrului ks și armarea se va stabili pe înfășurătoare.

Gruparea încărcărilor - stări limităîn calculul radierului -

      Distribuția încărcărilor variabile ce se consideră în gruparea fundamentală (GF) va fi stabilită pe o schemă cu probabilitatea cea mai mare de realizare în perioada de exploatare a construcției. Astfel se poate considera o distribuție variabilă pe înălțimea etajelor a valorii de calcul a acțiunii din exploatare (exemplu: (i)  STAS10101/2A1-89 jumătate din planșee -S+P+5, radier, placa de la cota ±0.00 și 5 planșee peste cota 0- se vor considera încărcate în șah, iar restul nivelelor vor fi, un plașeu încărcat complet și un planșeu fără încărcare utilă - în șah pe verticală-). Se pot propune și alte scheme, se recomandă ca rezultanta încărcările utile să nu fie mai mică decât situția în care toate planșeele sunt încărcate în șah cu încărcarea utililă normată.

Gruparea Fundamentală (GF)

În vederea stabilirii coeficientului de pat și a presiunilor de calcul, pentru gruparea fundamentală, se vor considera 3 ipoteze de încărcare:

a) Radier, placa de la cota ±0.00 și 5 planșee peste cota 0- se vor considera încărcate în șah, restul alternant pe verticală (planșeul cu încărcare completă și fără încărcare), încărcarea utilă fiind considerată acțiune predominantă;

 

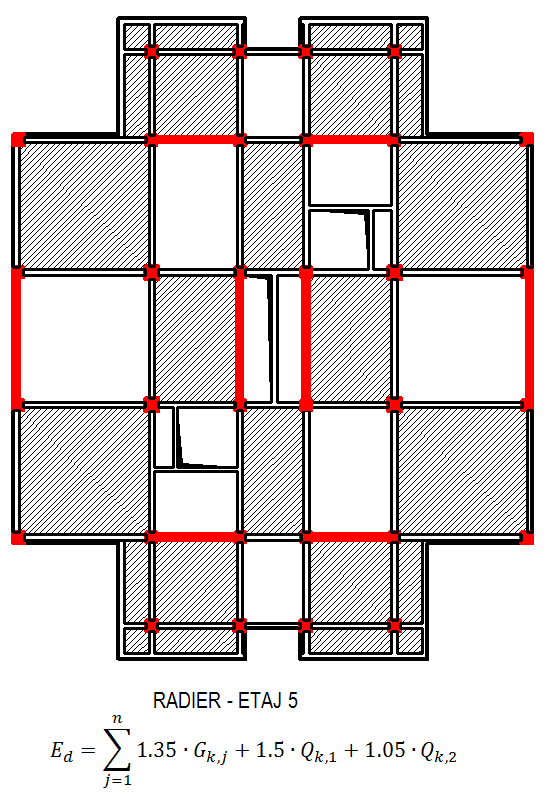
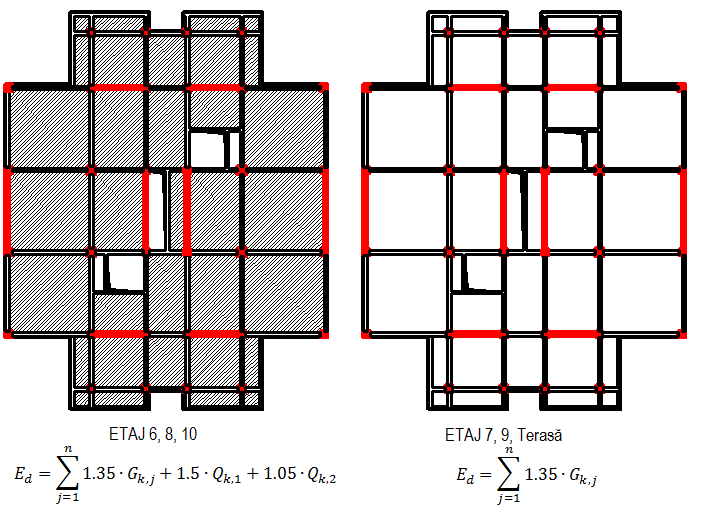
b) Toate planșeele încărcate uniform, gruparea de încărcare caracteristică;

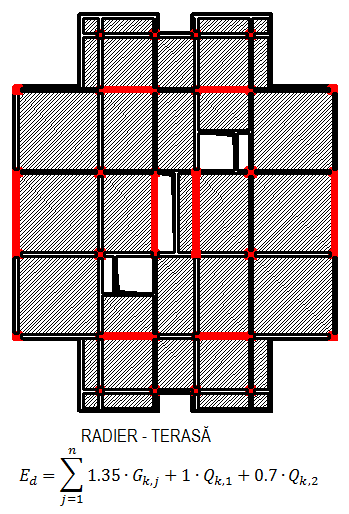
c) similar b, dar acțiunea din zăpadă cu efect predominant la nivelul terasei.

 În practica curentă se utilizează o singură ipoteză, SLU pentru plașeul curent valabilă pentru toate nivelurile. În anumite situații, în cazul construcțiilor mai mari de P+5E...7E, aceasta ducând la rezultate neverosimile (ipoteză: în viața unei construcții -categoria duratei de viață 4, 50ani...100ani- încidența ca pe toate planșeele pe întreaga construcție să se atingă starea limită ultimă este nulă). Ipoteza pleacă de la modul de încărcare a planșeelor și de la comportamentul utilizatorilor (oricine va sesiza o fisură amplă sau ruptură într-un element structural va părăsi imobilul sau va elibera planșeul).  Fisura sau ruptura într-un element structural apare în situația în care acesta a atins o anumită stare de exploatare (SLU sau SLS).

Gruparea Specială (GS)

În gruparea specială se va considera un singur caz pentru încărcările variabile (cvasipermanente) astfel:

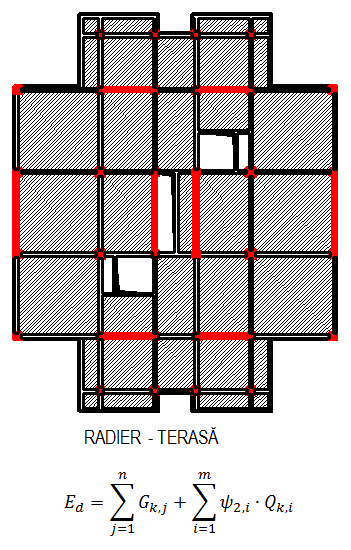
Stabilirea rigidității terenuluiși calculul stării de eforturi

   În calculul plăcilor pe mediu elastic se va ține seama de rigiditatea terenului (k_s=p/s, a se vedea calcul fundație izolată bloc și cuzinet punctul 8), rigiditatea resorturilor. Placa, radierul, se va discretiza în elemente pătrate, pe cât posibil, cu aria de 1mp. În nodurile acestora se vor introduce rigiditățile pe cele 3 direcții ( Z, X/Y, θ), pentru situațiile curente se poate opta doar pentru rigiditatea pe verticală (Z), rigiditate ce este dată de presiunea efectivă și tasarea, iar cele orizontale X și Y se pot bloca și cea de rotire θ fiind liberă, cu rigiditate nulă.

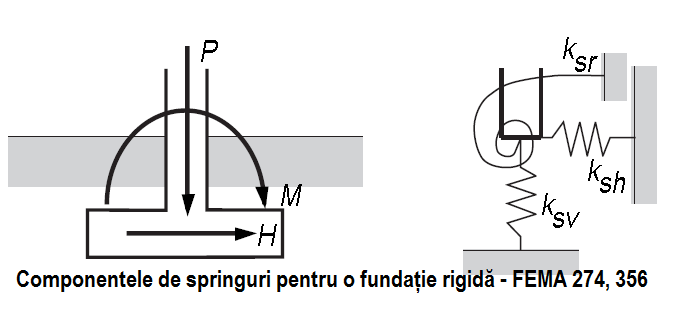
Rigiditatea pe verticală (Z) se poate stabili printr-un calcul aproximativ, urmând să se calibreze ulterior. Calculul aproximativ presupune evaluarea presiunii medii transmisă la nivelul terenului de sistemul structural prin intermediul radierului. Pentru structura dată sunt 13 planșee (inclusiv fundații -radier), se poate considera încărcare "topită"  în gruparea fundamentală (ipoteza 4.3.1. a/b) de 18kPa (această încărcare se poate determina exact), astfel rezultă o presiune medie de 234kPa. Pentru această presiune medie, cunoscând aria radierului, se determină tasarea efectivă, latura B=L=A_R^1/2. Pentru calcul tasare se poate consulta - calcul fundație izolată bloc și cuzinet punctul 6, pag. 15-19-. La structurile în cadre se poate considera o încărcare "topită" de 16kPa.

Calculul eforturilor se va face pe înfășurătoarea dată de grupările de calcul pentru diferite valori ale lui Ks. Ca mod de calcul, se dimensionează radierul în gruparea fundamentală pentru un Ks determinat sau dat în studiul geotehnic, iar pentru celelalte ipoteze se va face o verificare. În urma verificărilor se va dispune, sau nu, armătură suplimentară pe cele două fețe și direcții ale radierului. Convenția de semn pentru determinarea încovoierii, pentru majoritatea softurilor, urmărește regula "mâinii drepte", a se consulta [17, 18].

Rigiditatea springurilor de calcul:

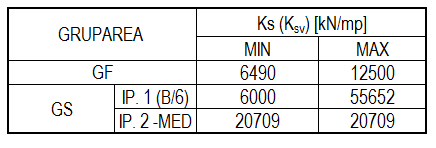
      Pentru Gruparea specială se poate merge pe o distribuție medie a coeficientului de pat sau pe împărțirea fundației în fâșii cu lățimea de B/6, unde B=A_R^1/2, a se consulta [6].

   

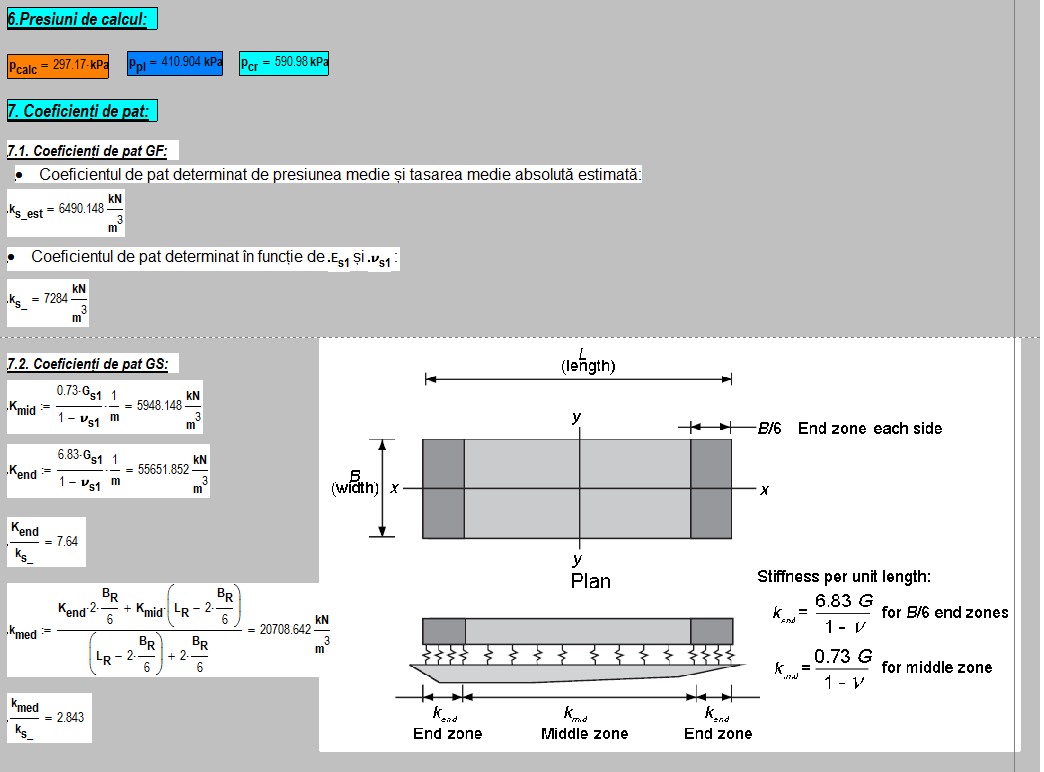
 Calculul se modifică în cazul terenurilor lichefiabile, sensibile la umezire sau la care influența apei subterane nu poate fi neglijată.

Se va face o primă verificare și dimensionare a radierului pentru K_s=6490 kN/mc pe întreg radierul în GF, și se va verifica pentru celelalte situații.

Se verifică: presiunea maximă < 1.2x297kPa; tasarea efectivă < 8cm; tasarea relativă < 6...2/1000. Dacă verificarea de tasare efectivă și presiune nu este îndeplinită se va trece la fundații indirecte, iar dacă verificarea de tasare relativă nu se îndeplinește se mărește înălțimea radierului.

Se propune: o armare pe cele două direcții sus și jos. În urma armării longitudinale se verifică la străpungere radierul, astfel se poate mări sau nu înălțimea radierului.

 

  

 

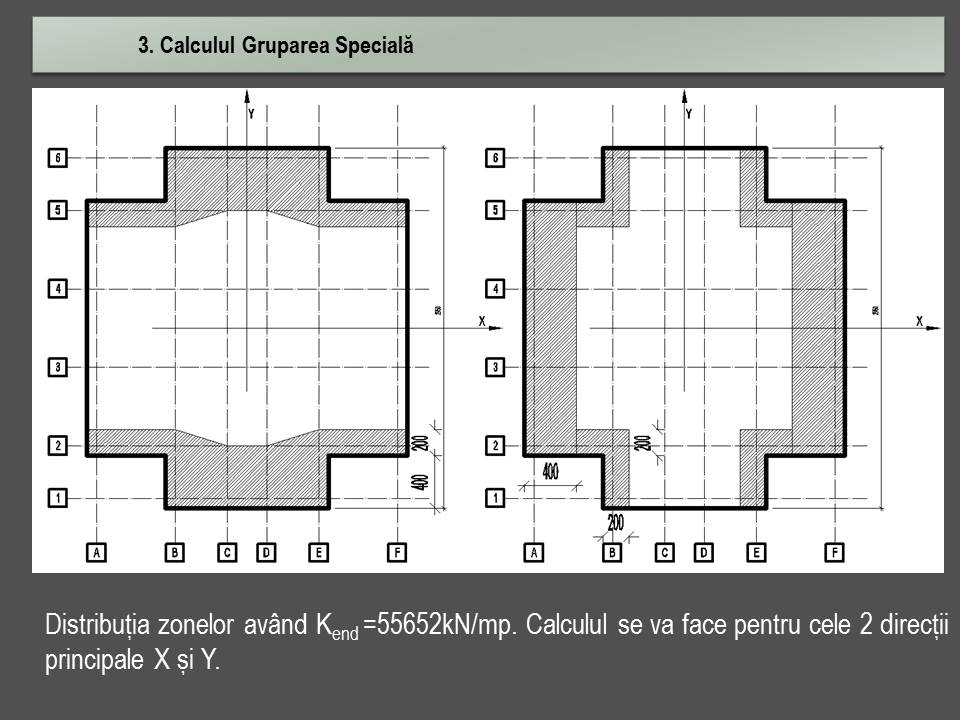
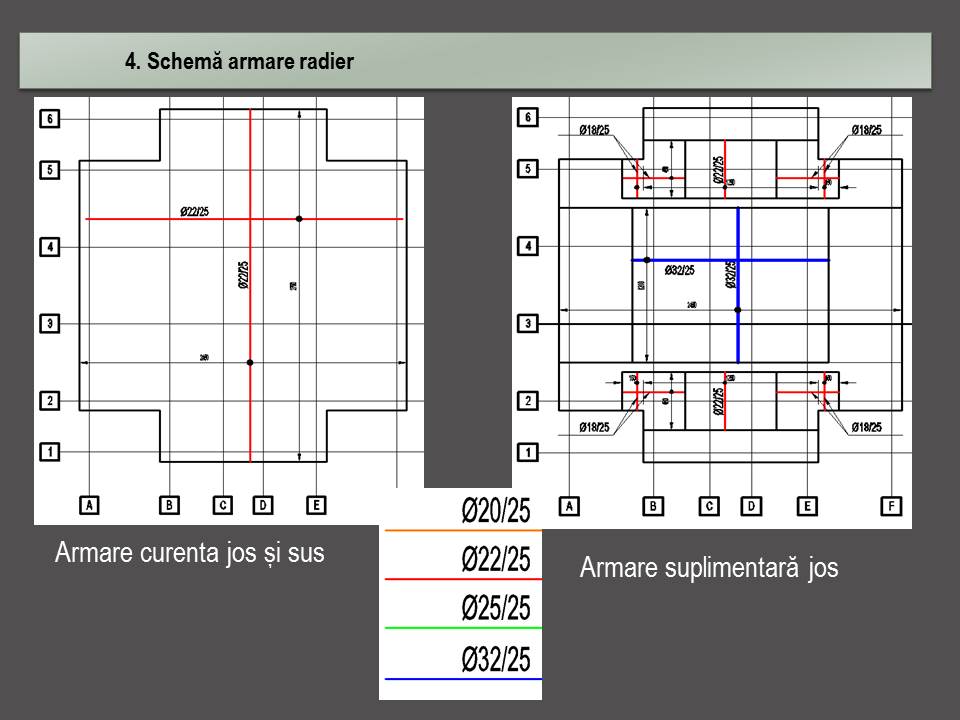
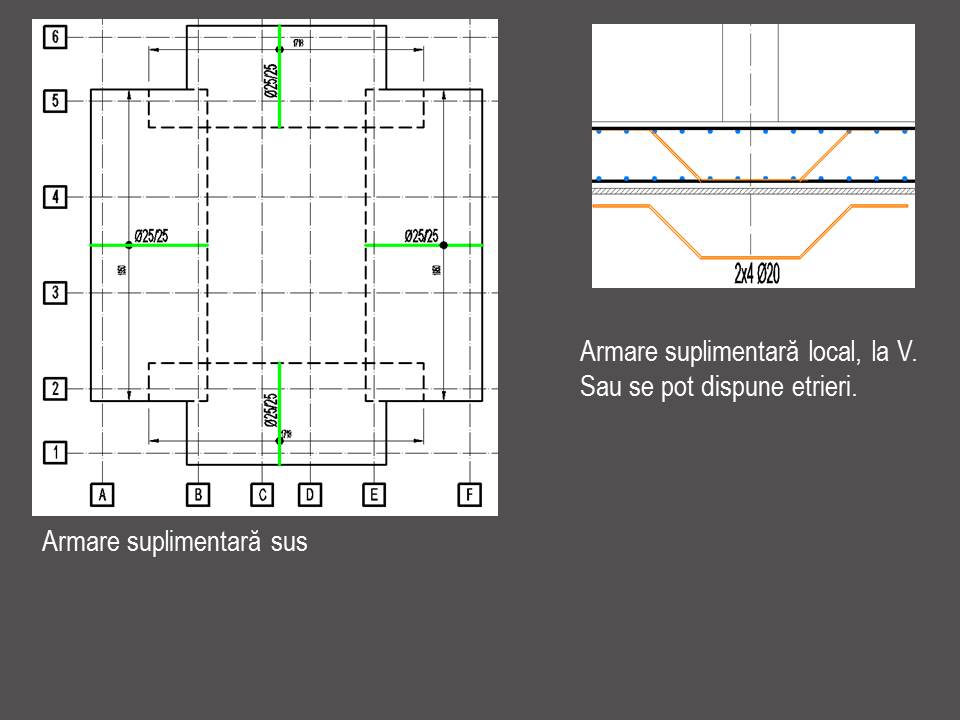
 Prezentare armare și calcul la încovoiere radier .

 

Bibilografie

1. CR2-1-1.1/2013 Cod de proiectare a construcțiilor cu pereți structurali de beton armat

2. NP112/2014 Normativ privind proiectarea fundațiilor de suprafață

3. Proiectarea structurilor de beton la acțiuni seismice, traducere L. Crainic. T. Paulay, H. Bachmann, K. Moser

4. P100-1/2013 Cod de proiectare seismică – Partea I – Prevederi de proiectare pentru clădiri

5. P100-3/2008 Prevederi pentru Evaluarea Seismică a Clădirilor Existente

6. FEMA 356 Prestandard and Commentary for the Seismic Rehabilitation of Buildings

7. Proiectarea structurilor de beton armat în zone seismice, vol. I, II, III, T. Postelnicu, I. Damian, D. Zamfirescu, E. Morariu, B. Buzăianu 

8. Calculul construcțiilor amplaste pe terenuri deformabile, Aurel A. Beleș, Clemansa Mihăilescu, Ștefan Mihăilescu

9. Calculul construcțiilor pe mediu elastic -1960, M.I. Gorbunov-Posadov 

10. NP122/2010 Normativ privind determinarea valorilor caracteristice și de calcul ale parametrilor geotehnici

11. GP129/2014 Ghid privind proiectarea geotehnică

12. GE029/1997 Ghid de proiecatre - Calculul terenurilor de fundare la acțiuni seismice în cazul fundării directe

13. Note de Curs - prof. dr. ing. Ion Radu Pascu

14. STAS 10107-0/90

15. STAS10101/2A1-89

16. STAS 3300-1,2/85

17. CSI Analysis Reference Manual

18. Calculul structurilor din beton armat cu programul ETABS, dr. ing. Iolanda-Gabriela Craifaleanu

19. SREN 1992-1-1/2004

20. Models for Punching Shear Capacity in Concrete Slabs, Ingeborg Skarholt Bølviken

21. Note de curs - Rezistența Materialelor- prof. ing. Panait Mazilu

22. Note de curs - Teoria Elasticității - prof. dr. ing. Dan-Ilie Crețu